Tato stránka vyžaduje podporu CSS stylů
4. domácí úloha z předmětu PAA
Experimentální hodnocení algoritmů pro řešení problému batohu
Oto Válek
FEL ČVUT, letní semestr 2001/2002, cvičení St 12:45
1. Specifikace úlohy
Problém
batohu
je řešen
hrubou sílou s
detekcí přetížení (1),
heuristikou cena/váha (2),
metodou větví a hranic (3),
dynamickým programováním (4)
a heuristikou podle poměru cena/váha s testem nejdražší věci (5).
Bližší popis metod viz řešení
1.úlohy a
3.úlohy
Sledována byla výpočetní náročnost a chyba řešení podle
zadání.
Čítač kroků řešení byl zvyšován na vhodném místě v hlavní rekurzivní funkci algoritmu.
U heuristik vybírajících nejvyšší poměr cena/váha byl navíc umístěn do cyklu
příslušné funkce, aby se projevila O(n) složitost pro každý navštívený stav.
U metody hrubé síly, dyn. programování a metody větví a hranic však počet kroků
zhruba odpovídá počtu navštívených stavů stavového prostoru.
Čas byl měřen funkcí ftime() ze std. C knihovny v prostředí WinNT.
Byl použit kompilátor z MS VC 5.0 s defaultním nastavením a procesor Intel Pentium 100 Mhz.
2. Testovací instance
Pro generování instancí byl použit zkompilovaný připravený
generátor.
Defaultní hodnoty parametrů byly zvoleny podle WWW formuláře:
-n 20 Velikost instance [10,15,20,25,30]
-N 50 Počet instancí
-W 100 Maximální váha věci
-C 250 Maximální cena věci [50,150,250,350,450]
-m 0.6 Poměr sumární váhy ke kapacitě batohu [0.2,0.4,0.6,0.8,1]
-d 0 Charakter granularity (-1 více malých, 1 více velkých) [-1,0,1]
-k 1 Exponent závislosti granularity
-I 0 Základní ID
Sledována byla závislost na vybraných parametrech, které nabývají následujích
hodnot (ostatní parametry na defaultních hodnotách) :
-n [10,15,20,25,30] Velikost instance
-C [50,150,250,350,450] Maximální cena věci
-m [0.2,0.4,0.6,0.8,1] Poměr sumární váhy ke kapacitě batohu
-d [-1,0,1] Charakter granularity (-1 více malých, 1 více velkých)
Každé hodnotě parametru odpovídá vygenerovaných 50 instancí,
v úvahu je brán aritmetický průměr.
3. Naměřené výsledky
Měřen byl reálný čas, počet kroků řešení, a relativní chyba proti
nejlepší nalezené ceně, kterou zde představuje výsledek metody dynamického
programování. U metody hrubé síly byl test ukončen pro n=20.
| | | | |
|
|---|
Čas řešení [ms]
|
| Hrubá
síla | Heuristika
cena/váha | Větve
a hranice | Dynamické
programování | Cena/váha
+ nejdražší
|
|---|
|
|
| Závislost na max. ceně věci C
|
| C=50 | 5912,7 | 0,2 | 45,9 | 608,2 | 0,6
|
|---|
| C=150 | 6003,0 | 0,4 | 41,3 | 598,4 | 0,8
|
|---|
| C=250 | 5360,7 | 0,4 | 41,1 | 596,9 | 0,6
|
|---|
| C=350 | 5533,6 | 1,2 | 40,1 | 600,2 | 0,6
|
|---|
| C=450 | 5615,5 | 1,0 | 36,7 | 597,1 | 0,8
|
|---|
|
|
| Závislost na granularitě instance d
|
| d=-1 (více malých) | 5507,5 | 0,6 | 35,9 | 629,4 | 0,8
|
|---|
| d=0 (rovnoměrně) | 5319,9 | 0,8 | 37,8 | 626,1 | 1,0
|
|---|
| d=1 (více velkých) | 5413,4 | 1,0 | 34,4 | 630,0 | 0,8
|
|---|
|
|
| Závislost na poměru sumární váhy ke kapacitě batohu m
|
| m=0.2 | 167,6 | 0,6 | 46,1 | 157,8 | 0,4
|
|---|
| m=0.4 | 2345,0 | 0,2 | 112,8 | 409,2 | 0,0
|
|---|
| m=0.6 | 5523,0 | 1,6 | 36,7 | 626,7 | 0,6
|
|---|
| m=0.8 | 6229,8 | 0,2 | 5,0 | 802,1 | 1,0
|
|---|
| m=1 | 6292,4 | 1,2 | 0,6 | 876,1 | 0,8
|
|---|
|
|
| Závislost na počtu věcí n
|
| n=10 | 5,0 | 0,0 | 0,8 | 48,1 | 0,2
|
|---|
| n=15 | 192,7 | 0,2 | 6,2 | 241,2 | 0,0
|
|---|
| n=20 | 5382,1 | 0,0 | 44,5 | 609,9 | 0,8
|
|---|
| n=25 | | 0,6 | 279,4 | 1193,5 | 1,0
|
|---|
| n=30 | | 0,8 | 2241,2 | 2141,2 | 1,4
|
|---|
Kroků řešení
|
| Hrubá
síla | Heuristika
cena/váha | Větve
a hranice | Dynamické
programování | Cena/váha
+ nejdražší
|
|---|
|
|
| Závislost na max. ceně věci C
|
| C=50 | 918187 | 307 | 6644 | 5873 | 327
|
|---|
| C=150 | 918187 | 303 | 5932 | 5873 | 323
|
|---|
| C=250 | 918187 | 302 | 5903 | 5873 | 322
|
|---|
| C=350 | 918187 | 307 | 5750 | 5873 | 327
|
|---|
| C=450 | 918187 | 307 | 5183 | 5873 | 327
|
|---|
|
|
| Závislost na granularitě instance d
|
| d=-1 (více malých) | 921353 | 305 | 4941 | 5958 | 325
|
|---|
| d=0 (rovnoměrně) | 920454 | 303 | 5142 | 5927 | 323
|
|---|
| d=1 (více velkých) | 921353 | 305 | 4941 | 5958 | 325
|
|---|
|
|
| Závislost na poměru sumární váhy ke kapacitě batohu m
|
| m=0.2 | 26624 | 171 | 6545 | 1943 | 191
|
|---|
| m=0.4 | 374711 | 239 | 16176 | 4244 | 259
|
|---|
| m=0.6 | 920454 | 303 | 5142 | 5927 | 323
|
|---|
| m=0.8 | 1046000 | 368 | 412 | 6910 | 388
|
|---|
| m=1 | 1048575 | 420 | 20 | 7153 | 440
|
|---|
|
|
| Závislost na počtu věcí n
|
| n=10 | 875 | 84 | 91 | 573 | 94
|
|---|
| n=15 | 28733 | 176 | 855 | 2663 | 191
|
|---|
| n=20 | 918187 | 302 | 5903 | 5873 | 322
|
|---|
| n=25 | | 466 | 37495 | 10230 | 491
|
|---|
| n=30 | | 670 | 319911 | 15657 | 700
|
|---|
Relativní zhoršení proti nejlepší možné ceně
|
| Hrubá
síla | Heuristika
cena/váha | Větve
a hranice | Dynamické
programování | Cena/váha
+ nejdražší
|
|---|
|
|
| Závislost na max. ceně věci C
|
| C=50 | 0,00% | 1,30% | 0,00% | 0,00% | 1,30%
|
|---|
| C=150 | 0,00% | 1,53% | 0,00% | 0,00% | 1,53%
|
|---|
| C=250 | 0,00% | 1,57% | 0,00% | 0,00% | 1,57%
|
|---|
| C=350 | 0,00% | 1,29% | 0,00% | 0,00% | 1,29%
|
|---|
| C=450 | 0,00% | 1,35% | 0,00% | 0,00% | 1,35%
|
|---|
|
|
| Závislost na granularitě instance d
|
| d=-1 (více malých) | 0,00% | 1,23% | 0,00% | 0,00% | 1,23%
|
|---|
| d=0 (rovnoměrně) | 0,00% | 1,42% | 0,00% | 0,00% | 1,42%
|
|---|
| d=1 (více velkých) | 0,00% | 1,23% | 0,00% | 0,00% | 1,23%
|
|---|
|
|
| Závislost na poměru sumární váhy ke kapacitě batohu m
|
| m=0.2 | 0,00% | 3,59% | 0,00% | 0,00% | 3,59%
|
|---|
| m=0.4 | 0,00% | 3,20% | 0,00% | 0,00% | 3,20%
|
|---|
| m=0.6 | 0,00% | 1,42% | 0,00% | 0,00% | 1,42%
|
|---|
| m=0.8 | 0,00% | 0,50% | 0,00% | 0,00% | 0,50%
|
|---|
| m=1 | 0,00% | 0,00% | 0,00% | 0,00% | 0,00%
|
|---|
|
|
| Závislost na počtu věcí n
|
| n=10 | 0,00% | 2,60% | 0,00% | 0,00% | 2,60%
|
|---|
| n=15 | 0,00% | 1,72% | 0,00% | 0,00% | 1,72%
|
|---|
| n=20 | 0,00% | 1,57% | 0,00% | 0,00% | 1,57%
|
|---|
| n=25 | | 1,22% | 0,00% | 0,00% | 1,22%
|
|---|
| n=30 | | 1,16% | 0,00% | 0,00% | 1,16%
|
|---|
4. Srovnání algoritmů
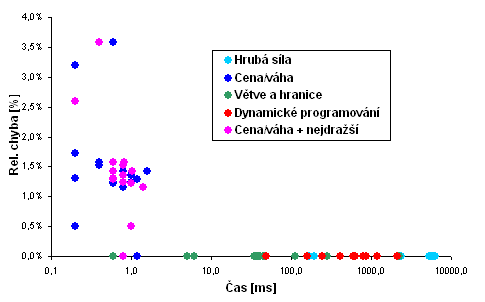
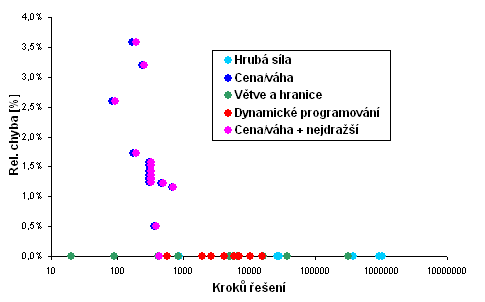
Následuje srovnání algoritmů podle výpočetní náročnosti a chyby řešení.
Každé měřené kombinaci parametrů generátoru odpovídá jeden bod v ploše
- průměr z 50 instancí. Čas je vynesen v logaritmickém měřítku.
5. Závěr
Závislost na max. ceně věci C
Změna maximální ceny věci činnost algoritmů v podstatě neovlivňuje. S vyššími
hodnotami cen se jen zvyšuje jakási "inflace" v úloze - i výsledná max. cena je vyšší.
Růst ceny (a tím především relativní zjemňování intervalu) prospívá jen v malé
míře metodě větví a hranic, jelikož ořezání podle optimalizačního kritéria
nastává dříve.
Chyba heuristických metod nabývá nevýrazného maxima pro C=250, pro což jsem
nenalezl vhodné vysvětlení.
Závislost na granularitě instance d
Překvapivé zjištění je, v žádném případě nehraje roli, zda převažují věci malé
nebo velké, podstatný je jen rozdíl mezi rovnoměrným a nerovnoměrným rozložením
vah věcí.
Ve výpočetní náročnosti výraznější rozdíly nejsou, heuristika se doupuší na
nerovnoměrně rozložených vahách věci menší chyby.
Závislost na poměru sumární váhy ke kapacitě batohu m
Tento parametr má na průběh algoritmů velmi podstatný vliv.
Menší hodnoty parametru (tj. "hodně věcí na výběr a malý batoh") vyhovují
hrubé síle a dynamickému programování. U těchto metod se dříve prosadí
kontrola přetížení batohu, která stavový prostor ořeže více právě v případě,
kdy je věcí o hodně více, než se jich do batohu vejde.
Metodě větví a hranic naopak vyhovuje případ, kdy se do batohu vejde většina
věcí. Vzhledem k tomu, že moje implementace v každém kroku nejprve věc přidává
je velmi brzy nastavena ořezávací hodnota opt. kritéria blízko max. ceny a
většina stavového prostoru se pak neprohledává.
Heuristika cena/váha má s rostoucí hodnotou parametru "stále méně na výběr" a
tedy "stále méně co zkazit" a tak relativní chyba klesá.
Závislost na počtu věcí n
Tato závislost je už podrobněji rozebrána ve
3. úloze.
Výpočetní náročnost hrubé síly je exponenciální. Totéž lze říci i o metodě
větví a hranic, i přes značné snížení počtu kroků. Přesto je v mé implementaci
výhodnější než dynamické programování pro instance menší než cca 22-33 věcí.
Metoda dynamického programování se ukázala nejvýhodnější pro vyšší n.
S rostoucím n se počet kroků blíží lineární závislosti.
Chyba heuristiky cena/váha s rostoucím počtem věcí klesá. Ubývá totiž zastoupení
"výjimek", které kazí zjednodušený pohled heuristiky na problém.
6. Soubory
4hodnoceni.zip - ZIP archiv zdrojových souborů v C++,
zadaných a naměřených hodnot, generátoru instancí, tohoto dokumentu a Excel. tabulky s analýzou dat.


