Tato stránka vyžaduje podporu CSS stylů

5. domácí úloha z předmětu PAA

Problém obchodního cestujícího

Oto Válek

FEL ČVUT, letní semestr 2001/2002, cvičení St 12:45

1. Specifikace úlohy

Klasický problém obchodního cestujícího je řešen metodou simulovaného ochlazování. Počáteční řešení je nalezeno greedy prohledáváním, obohaceném o operaci "prohození konce cesty", viz níže. Omezil jsem se na hledání cesty, která prochází každým městem právě jednou, délka cesty se pak během simulovaného ochlazování nemění.

K testování byly použity připravené instance a.txt .. k.txt a testik.txt. Algoritmus byl implementován v jazyce Perl. Byl použit Active Perl 5.005_03 pod Windows 2000 a procesor Intel Pentium III 1GHz.

2. Reprezentace grafu

Pro nepříliš husté grafy, které v testovaných instancích převažují, není uzlová metice nejvhodnější reprezentací. Proto informaci o sousedících uzlech každého uzlu uchovávám v polích sousedů, seřazených podle délky hrany. Informace o délkách hran je uložena v poli asociativních polí (tzv hash).

Načtený graf je podroben ořezávání, které má za cíl zjistit, zda nelze existenci Hamiltonovy kružnice předem vyloučit:

kontrola, zda mají všechny uzly stupeň alespoň 2
u uzlů, které mají právě 2 sousedy stupně 2, odstraníme ostatní hrany
kontrola, zda neexistují uzly s více než 2 sousedy stupně 2
kontrola, zda je graf souvislý

Během procházení stavovým prostorem je aktuálním stavem cesta reprezentovaná rovněž polem čísel uzlů. Perl pak umožňuje poměrně jednoduše realizovat použité operace:

  push(@kruznice,reverse splice(@kruznice,$i));                  ### prohození od indexu $i
  splice(@kruznice,$i+1,0,reverse splice(@kruznice,$i+1,$j-$i)); ### dvouzáměna mezi $i,$j

3. Nalezení počátečního řešení

Simulované ochlazování je iterativní algoritmus, který potřebuje počáteční řešení, aby ho by mohl vylepšovat. Je tedy třeba pokud možno rychle najít Hamiltonovu kružnici libovolné délky. Samozřejmě je lepší, pokud algoritmus jejího nalezení bude preferovat použití hran kratších délek.

Pro nalezení Hamiltonovy kružnice je použit upravený greedy algoritmus, tedy prohledávání bez návratu. V každém stavu se algoritmus pokusí dosud sestavenou cestu prodloužit o souseda, který v cestě dosud není. Vybírá je přitom ze seznamu seřazeného podle vzdálenosti z aktuálního uzlu. Tím je dosaženo preferování kratších cest.

Aby byla do tohoto procesu vnesena náhoda, a při každém spuštění se došlo k jinému výchozímu řešení, s pravděpodobností 10% je vybrán druhý nejbližší, namísto prvního nejbližšího souseda. Počátečním uzlem prohledávání je uzel s nejvyšším stupněm. Uzavření kružnice v takovém uzlu by pak mělo být nejsnažší.

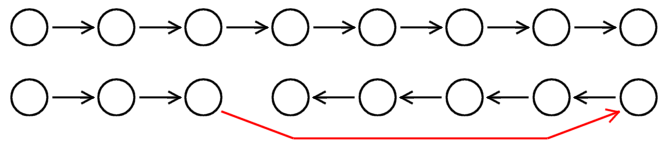
Pokud již nelze cestu z posledního uzlu prodloužit, algoritmus zkusí použít operaci "prohození". Mezi těmi sousedy posledního uzlu, které již v cestě jsou, vybere náhodně jeden, a cestu za ním obrátí a připojí koncovým uzlem k němu. Takto se změní poslední uzel a je možno pokračovat dále. Viz následující schéma:

4. Simulované ochlazování

Schéma metody simulovaného ochlazování se dá popsat tímto kódem:

stav = pocatecni_stav;
teplota = pocatecni_teplota;
repeat {
  repeat {
    stav = try(teplota, stav);
  } until equilibrium();
  teplota = cool(teplota);
} until frozen(teplota);

Teplota zde představuje pravděpodobnost přijetí horšího řešení při procházení stavového prostoru. V průběhu vypočtu teplota klesá - a klesá také schopnost překonávat lokální minima.

Operace dvouzáměny

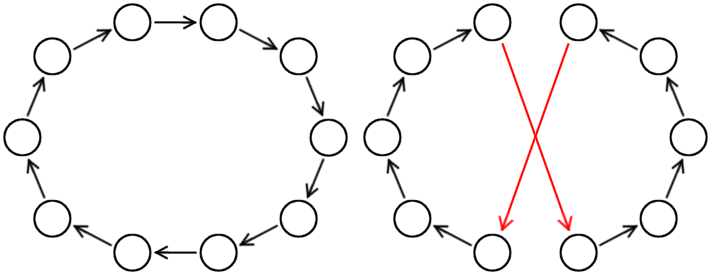
Moje implementace uvažuje pouze 2-okolí stavu, tedy operaci dvouzáměny (viz obrázek niže). Protože se provádí jen když existují příslušné hrany (označené červenými šipkami), pohybuje se tak algoritmus stále v prostoru přípustných řešení.

Počáteční teplota

Počáteční teplota je určena pokusným zahříváním. Začínáme na nízké teplotě t=1 a zvyšujeme ji v geometrické řadě s podle předpisu t_n+1=1.1*t_n. Pokračujeme, dokud není průměrná četnost přijetí horšího řešení vyšší než 15%. Tuto průměrnou četnost zjistíme 50-ti násobným provedením operace try(). Protože u některých instancí četnost velice dlouho nedosahovala požadované hodnoty, doplnil jsem ještě ukončení této fáze o další podmínku - dosažení teploty t=1000.

Po zjištění počáteční teploty je obnoven předchozí stav, tedy kružnice nalezená jako počáteční řešení a teplota je nastavena na právě zjištěnou počáteční.

Ochlazování

Snižování teploty probíhá geometrickou řadou podle předpisu t_n+1=0.8*t_n. V každém průchodu je 50-krát provedena funkce try(). Funkce equilibrum() je zde tedy pevný počet opakování.

Funkce try()

Funkce try() má následující obecnou strukturu (rand() vrací číslo v intervalu <0,1) ):

sub try (teplota,stare) {
  nove = nahodny_soused(stare);
  delta = cena(nove)-cena(stare);
  if (delta<=0) return nove;
  elsif (rand()<exp(-delta/teplota)) return nove;
  else return stare;
}

Cenovou funkci ohodnocující řešení v našem případě představuje délka příslušné kružnice. Funkce nahodny_soused() zde provede dvouzáměnu u dvou dvojic náhodně vybraných uzlů. Nejprve vybere náhodně uzel na kružnici a pak vybere náhodně z jeho sousedů v grafu. Je to tak efektivnější, než náhodně vybrat dva uzly, a pak testovat, zda sousedí, a to zejména u řídkých grafů.

Ukončení ochlazování - funkce frozen()

Ukončení ochlazování jsem nezvolil závislé na teplotě. Cyklus snižování teploty je ukončen, pokud se v 10 po sobě následujících průchodech řešení nezlepšilo ani nezhoršilo. Stane se tak tedy až po 50*10=5000 neúspěšných voláních fce try(). Ve většině řešených instancí se tak stalo při teplotě menší než 0.001.

5. Naměřené výsledky

Následují výsledky naměřené na testovacích instancích ve třech variantách ohodnocení "neexistujících hran". Počet prošlých stavů je počítán jako počet jen těch případů, kdy funkce try() vrátila nové řešení, ať už horší či lepší. Proto se muže někdy zdát nízký.

1) neexistující hrany mají ohodnocení 10

Zde nebylo simulované ochlazování téměř vůbec úspěšné. Jedná se totiž o úplné grafy, a zde už úvodní greedy algoritmus dokáže najít velmi dobré řešení, na kterém pak není co vylepšovat. Parametry simulovaného ochazování jsem se navíc snažil vyladit pro případ 3), který je typičtější.


	počáteční řešení	koncové řešení	zlepšení	prošlých stavů
a.txt	18810	18835	-0,13%	483	2187 uzlů
b.txt	2871	2973	-3,55%	350	625 uzlů
c.txt	20231	20262	-0,15%	753	2187 uzlů
d.txt	581	602	-3,61%	49	200 uzlů
e.txt	875	703	19,66%	748	256 uzlů
f.txt	19991	20025	-0,17%	879	2187 uzlů
g.txt	12475	12818	-2,75%	6725	1296 uzlů
h.txt	781	849	-8,71%	463	236 uzlů
i.txt	14957	15024	-0,45%	57	2187 uzlů
j.txt	19507	19532	-0,13%	655	2048 uzlů
k.txt	12156	12733	-4,75%	5894	1296 uzlů
testik.txt	172	193	-12,21%	314	81 uzlů

2) neexistující hrany mají ohodnocení 10000

Při ohodnocování neexistujících hran vysokou hodnotou by se dalo očekávat, že je simulované ochlazování postupně odstraní. V našem případě se tak tomu nestalo. Počet odtraněných nekonečných hran se pohyboval v jednotkách.

Je možné, že použitá operace try() a náhodná dvouzáměna nedokáže tato výrazná zlepšení dostatečně preferovat. Pro funkci try() je totiž každé zlepšení stejně dobré.


	počáteční řešení	koncové řešení	zlepšení	prošlých stavů
a.txt	5960894	5950903	0,17%	437	2187 uzlů
b.txt	271909	272097	-0,07%	132	625 uzlů
c.txt	14305289	14305289	0,00%	2251	2187 uzlů
d.txt	90664	41189	54,57%	137	200 uzlů
e.txt	80527	41121	48,94%	157	256 uzlů
f.txt	13555992	13546016	0,07%	2307	2187 uzlů
g.txt	10301291	10251314	0,49%	2419	1296 uzlů
h.txt	190478	190764	-0,15%	116	236 uzlů
i.txt	21510249	21510249	0,00%	4106	2187 uzlů
j.txt	4905749	4865798	0,81%	189	2048 uzlů
k.txt	9102017	9002111	1,10%	1174	1296 uzlů
testik.txt	208	205	1,44%	251	81 uzlů

3) neexistující hrany skutečně neexistují

Zde je patrné, že simulované ochlazování s operací dvouzáměny je vhodné spíše pro hustší grafy. V grafech se stupni uzlů 4-7 je také graf stavového prostoru vzhledem k této operaci řídký, a tak se ani při vysoké teplotě nedostane algoritmus ve stavovém prostoru "daleko". Je také možné, ač jsem to netestoval, že pak prohledávání navštíví mnoho stavů vícekrát. V těchto grafech pak docházelo dokonce ke zhoršení výsledku.

V instanci i.txt, která se skládá z uzlů stupně 3, nedokázalo úvodní greedy prohledávání ani po delší době nalézt Hamiltonovu kružnici. V grafech instancí g.txt a h.txt pak ani Hamiltonova kružnice existovat nemůže.


	počáteční řešení	koncové řešení	zlepšení	prošlých stavů
a.txt	18782	18827	-0,24%	5979	2187 uzlů, do stupně 10, hlavně 4-5
b.txt	2646	2106	20,41%	5289	625 uzlů, nejvíce se stupněm 30-45
c.txt	17730	17730	0,00%	4200	2187 uzlů, do stupně 10, hlavně 4-5
d.txt	713	692	2,95%	1533	200 uzlů, nejvíce se stupněm 30-37
e.txt	647	610	5,72%	1667	256 uzlů, nejvíce se stupněm 30-40
f.txt	18375	18379	-0,02%	4495	2187 uzlů, do stupně 15, hlavně 5-7
g.txt	HK neexistuje (uzel se 3 sousedy stupně 2 během ořezávání)				1296 uzlů, do stupně 7, hlavně 2-4
h.txt	HK neexistuje (uzel stupně 1)				236 uzlů, 1 uzel má stupeň 1
i.txt	HK nenalezena				2187 uzlů, téměř výhradně stupně 3
j.txt	22021	21957	0,29%	10855	2048 uzlů, nejvíce se stupněm 17-22
k.txt	12819	12819	0,00%	4643	1296 uzlů, do stupně 13, hlavně 4-6
testik.txt	215	207	3,72%	441	81 uzlů, téměř úplný graf, stupně 62-77

Testované instance podle ceny nalezeného řešení

Zde je pořadí testovaných instancí podle ceny nejlepšího nalezeného řešení. Jedná se o případ 3), kdy hrany ohodnocené nulou neexistují. Pořadí podle počátečního řešení i koncového řešení je shodné.


	počáteční řešení	koncové řešení	zlepšení	prošlých stavů
testik.txt	215	207	3,72%	441	81 uzlů, téměř úplný graf, stupně 62-77
e.txt	647	610	5,72%	1667	256 uzlů, nejvíce se stupněm 30-40
d.txt	713	692	2,95%	1533	200 uzlů, nejvíce se stupněm 30-37
b.txt	2646	2106	20,41%	5289	625 uzlů, nejvíce se stupněm 30-45
k.txt	12819	12819	0,00%	4643	1296 uzlů, do stupně 13, hlavně 4-6
c.txt	17730	17730	0,00%	4200	2187 uzlů, do stupně 10, hlavně 4-5
f.txt	18375	18379	-0,02%	4495	2187 uzlů, do stupně 15, hlavně 5-7
a.txt	18782	18827	-0,24%	5979	2187 uzlů, nejvíce se stupněm 11-19
j.txt	22021	21957	0,29%	10855	2048 uzlů, nejvíce se stupněm 17-22
g.txt	HK neexistuje (uzel se 3 sousedy stupně 2 během ořezávání)				1296 uzlů, do stupně 7, hlavně 2-4
h.txt	HK neexistuje (uzel stupně 1)				236 uzlů, 1 uzel má stupeň 1
i.txt	HK nenalezena				2187 uzlů, téměř výhradně stupně 3

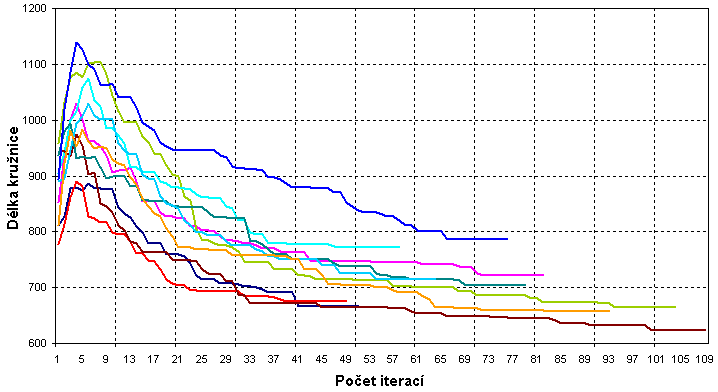
Průběh délky kružnice během ochlazování

Do grafu je vyneseno 10 průběhů řešení instance d.txt pro případ 3) neexistence hran ohodnocených nulou. Jako jedna iterace se zde počítá jedno snížení teploty, tedy 50 volání funkce try(). Je vidět, že různě dobrá počáteční řešení dávají různé výsledky, tedy že určitá závislost existuje. Také průběh délky během ochlazování je podobný, maximum bývá mezi 4-7 iterací. Patrná je i podmínka 10 iterací beze změny, která ochlazování ukončuje.

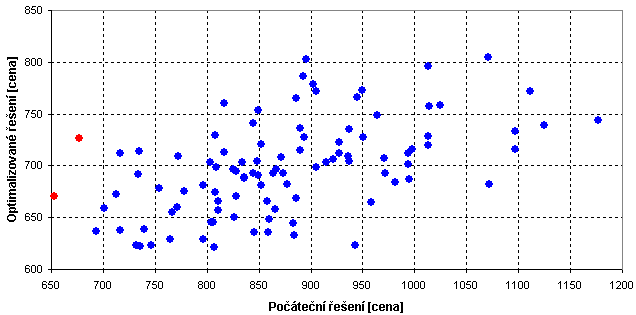
Závislost výsledného řešení na počátečním

Každý bod odpovídá jednomu ze 100 řešení instance d.txt. V grafu je možné vysledovat nevýraznou závislost, že horším počátečním řešením spíše odpovídají horší výsledná. Jinak je ale patrný vliv náhodného rozhodování ve všech fázích algoritmu. Ve dvou ze 100 případů došlo dokonce při simulovaném ochlazování ke zhoršení.

Závislost ceny počátečního a koncového řešení

6. Závěr

Problém obchodního cestujícího jsem řešil metodou simulovaného ochlazování, tedy pokročilou iterativní metodou vylepšující nějaké předem známé řešení. Přestože jsem se snažil parametry algoritmu co nejlépe vyladit, některé instance, zejména velkých málo hustých grafů, se zlepšit nepodařilo.

Důvodem muže být poměrně dobré počáteční řešení nalezené úvodním greedy prohledáváním. Dalo by se také uvažovat o záměně tří hran (uvažuje 3-okolí bodu) místo dvouzáměny. Tato silnější operace by se mohla po "stísněném" stavovém prostoru řídkých grafů pohybovat snáze.

7. Soubory

5tsp.zip - ZIP archiv zdrojového souboru v Perlu, instancí a logů výpočtu, tohoto dokumentu a Excel. tabulky s analýzou dat.

5. domácí úloha z předmětu PAA Problém obchodního cestujícího Oto Válek